He’d come to understand the tongues of beasts at the cost of his reason, while I was destroying human language to reveal the river of nonsense coursing just beneath its “good, sound rules.”
Ben Lerner, The Topeka School
I.
Language is a tool for communication. But for it to be a tool that can act as a medium, that tool must be concomitant with a set of rules that participating parties agree on and know ahead of time. Creating a system like this is often called a formalization. Formalizations are often delineated along an axis of syntax and semantics. Syntax consists of the rules in practice, and a system’s semantics are the meaning we get by using that system. In the world of the foundations of mathematics or analytic philosophy, you may see a diagram that looks like this:
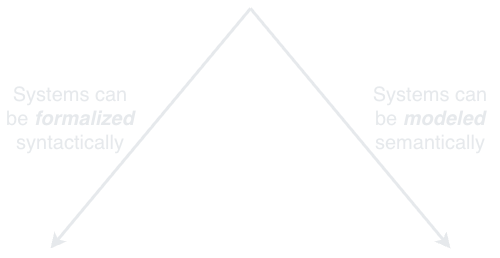
These pillars tame entropy into information, without them, the signal is lost to the noise.
II.
Formalization like this is hard, because signifying an intuition through a syntax is inherently a limiting action. Ideas, intuitions, emotions, all of these exist in a continuous, entropic space, unbroken by the discretizing force of syntax. When we attempt to relate an idea via speech or writing, that continuous space must be reduced into differentiable pieces. Deleuze and Guattari wrote about this phenomenon and termed it “territorializing”. To get a grip on their concept, think of a pristine, undiscovered continent. Upon discovery, its (assumption: capitalist) discoverers break the land up arbitrarily such that it may be classified as states, countries, counties, or even parcels of land to be sold. This is a material example of territorializing. But Deleuze and Guattari didn’t stop there—they abstracted territorializing and found limitless applications. Language itself is a territorializer to our thoughts. Their most famous work, the Capitalism and Schizophrenia series, discusses a “critical schizophrenia”. At its core, it is a rejection of Freudian psychoanalysis. They saw Freud’s battle with schizophrenia to truly be about the assimilation of the analysand. D&G’s critical schizophrenia refers to the untethered and unassimilated analysand—to a mind deterritorialized. Language, according to Deleuze and Guattari, is a gilded cage for your thoughts.

“There are things that are not sayable, that’s why we have art.” - Leonora Carrington (La maja del tarot, 1965)
D&G’s isn’t the only attempt to articulate such a phenomenon. It, albeit in different terms, is also discussed in Bernard Steigler’s book For a New Critique of Political Economy. Steigler makes the point that the very act of writing a practice down, i.e., externalizing it from one’s mind, is a tool for oppression. His argument is that hypomnesis, the exteriorization of memory, induces the possibility of a management class. Hypomnesis’ antonym, anamnesis, refers to internalized recollection or reference, without the need for external aids. In a world primarily driven by anamnesis, each generation learns its trade, its means for survival, from the one that came before it. Knowledge is passed down directly, its purpose is for the survival and the flourishing of generations to come. The point that Stiegler is trying to make is that hypomnesis is how a managerial class can invent itself, without the abstraction of exteriorization there cannot be the abstraction of a managerial class; the two are inextricably combined. Steigler’s is a Marxist argument: the territorialization of generational knowledge is a cornerstone in separating real value from use value, precisely through that generative abstraction.
III.
I think Steigler is right w/r/t grammatization (his term for what we’ve been calling territorializing) being a crucial tool for the oppression of the working class, however, his theory’s veracity is in my opinion, governed by the intent of the grammarizer. If you take Steigler’s argument as I understand it to its terminus, you arrive at a kind of ludditic anarcho-primitivism. This is in contradiction with a different type of syntax, the syntax of mathematics, whose goal is to universalize access to precise information. When we externalize a mathematical thought through syntax, it isn’t for oppression, it’s to verify. Without a reduction in fidelity, nothing could be checked; not just because verification inherently entails exteriorization, but also because to verify infinity, you would first need to calculate it. However, if we can signify infinity in the finite through syntax, we can verify it as well. In fact, we can even ask a computer to verify it for us by presenting the computer its own syntax—a set of rules—which can be used to interpret and then validate the syntax we’ve input. This is of course something a computer can do faster and with greater precision than we can as humans for many reasons, not the least of which is that a computer does not suffer the loss of fidelity or struggle to discretize intuition because its entire existence is resident in the world of syntax. What is a computer besides a territorializer of electrons, anyway?
What is a computer besides a territorializer of electrons, anyway?
An example: The notion that a + b = b + a is something we intuitively know, we’ve known it since not long after we learned addition. This law is called commutativity, it generalizes the idea of flipping operands and ending up with the same result. Below is a proof of the commutativity of addition on the natural numbers.
+-identᵣ : ∀ (a : ℕ) → a + zero ≡ a
+-identᵣ zero = refl
+-identᵣ (succ a) = cong succ (+-identᵣ a)
+-succ : ∀ (a b : ℕ) → (succ a) + b ≡ a + (succ b)
+-succ zero b = refl
+-succ (succ a) b = cong succ (+-succ a b)
+-comm : ∀ (a b : ℕ) → a + b ≡ b + a
+-comm zero b = sym (+-identᵣ b)
+-comm (succ a) b = trans (cong succ (+-comm a b)) (+-succ b a)This proof, in a way, calculates infinity. The natural numbers are, after all, an infinite set. The last stanza, those three lines that begin with +-comm, comprise the commutativity proof, the other two stanzas are lemmas needed to complete the final proof. This, to me, is irrefutable evidence of the limiting nature of syntax. It’s through syntax, with which we signify infinity, that we can begin to wrestle with it.
IV.
Another almost-articulation of this is Kant’s analytic and synthetic divide. I’ll quote the SEP:
“Analytic” sentences, such as “Pediatricians are doctors,” have historically been characterized as ones that are true by virtue of the meanings of their words alone and/or can be known to be so solely by knowing those meanings. They are contrasted with more usual “synthetic” sentences, such as “Pediatricians are rich,” (knowledge of) whose truth depends also upon (knowledge of) the worldly fortunes of pediatricians.
What we have above is an analytic proof of the commutativity of addition. Its synthetic proof, one more representative of our intuition, would require infinite time and infinite resources. The synthetic proof requires us to run every possible combination of pairs of natural numbers, effectively squaring infinity. Now, obviously, synthetic / analytic are not the same as the phenomenon of syntax’s discretizing force. It would of course still be syntax that we’d use to calculate infinity if we had infinite time to calculate it. Like the sentences you’re reading here, we’d be using syntax to bridle infinity. My goal instead is to articulate that all of these concepts are related, somehow, but that we lack the medium through which to elucidate exactly how. The notion of an unobtainable medium evinces St. Anselm’s argument for the existence of God (again, from the SEP):
St. Anselm reasoned that, if such a being fails to exist, then a greater being—namely, a being than which no greater can be conceived, and which exists—can be conceived. But this would be absurd: nothing can be greater than a being than which no greater can be conceived. So a being than which no greater can be conceived—i.e., God—exists.
St. Anselm’s ontological argument makes the case that God is that unattainable
medium. It’s a medium, a being, a notion, a thought that’s unscratchable by our
feeble minds. In an epigraph from Ursula Le Guin’s The Lathe of Heaven she
quotes Zhuang ZhouThis quote has come to be known as a bad translation. At the time of
its writing, the lathe had not been invented yet.
:
To let understanding stop at what cannot be understood is a high attainment. Those who cannot do it will be destroyed on the lathe of heaven.
It’s this that makes art feel holy. It’s this that motivates why grappling with the foundations of math ensnares me in such a way that I can lose time, whole hours, when I’m given to its chase. It’s this that is the explanation for the chill I’m feeling as I type this—I’m reaching out to something I cannot see but am absolutely compelled by. Something I can only picture through a glass, darkly. The thrill of the pursuance of God.
Moses said, “Show me your glory, I pray.” And he said, “I will make all my goodness pass before you, and will proclaim before you the name, ‘The Lord’; and I will be gracious to whom I will be gracious, and will show mercy on whom I will show mercy. But,” he said, “you cannot see my face; for no one shall see me and live.”
Exodus 33:18-20 (NRSV)