Cryptography 🤝 Vectorization

Using AES-XTS as a lens into vectorization techniques.

Cryptography 🤝 Vectorization

Using AES-XTS as a lens into ~~vectorization~~ parallelization techniques.

Agenda

What is AES and how does it work?
What is XTS and how does it work?
Vectorization 101
Vectorization in the real world
Bonus optimizations

AES

AES is the Advanced Encryption Standard, defined in FIPS 197 published in 2001.

It is a symmetric key block cipher algorithm that works on 16-byte blocks.
It’s the underlying encryption used in technologies like SSL/TLS.

AES

AES comes in different flavors whose distinction is the size of the key: 128, 192, or 256 bits.

Before [[en|de]]cryption, keys are expanded into “round keys”, leaving the only difference between AES-[[128|192|256]] to be the number of rounds:

128 bits has 10 rounds
192 bits has 12 rounds
256 bits has 14 rounds

AES

What is meant by “round”?

Each round has 4 transformations: SubBytes, ShiftRows, MixColumns, and AddRoundKey. The algorithm runs each of these transformations on the 16-byte state block for \(n\) rounds.

round :: [Word32] -> [Word32] -> [Word32]
round rk = addRoundKey rk . mixColumns . shiftRows . subBytes

roundLast :: [Word32] -> [Word32] -> [Word32]
roundLast rk = addRoundKey rk . shiftRows . subBytes

encrypt_ :: [Word32] -> [Word32] -> [Word32]
encrypt_ plain expandedKey =
  go (addRoundKey (take 4 expandedKey)
     (matrify plain)) (drop 4 expandedKey) 1
  where
    go :: [Word32] -> [Word32] -> Int -> [Word32]
    go state ek 14 = matrify $ roundLast ek state
    go state ek i = go (round (take 4 ek) state) (drop 4 ek) (i + 1)

AES

What is meant by “round”?

Intel VAES-NI implements a single round with vaes[enc|dec]:

vpxor	($key2), $state, $state
vaesenc	0x10($key2), $state, $state
vaesenc	0x20($key2), $state, $state
vaesenc	0x30($key2), $state, $state
vaesenc	0x40($key2), $state, $state
vaesenc	0x50($key2), $state, $state
vaesenc	0x60($key2), $state, $state
vaesenc	0x70($key2), $state, $state
vaesenc	0x80($key2), $state, $state
vaesenc	0x90($key2), $state, $state
vaesenc	0xa0($key2), $state, $state
vaesenc	0xb0($key2), $state, $state
vaesenc	0xc0($key2), $state, $state
vaesenc	0xd0($key2), $state, $state
vaesenclast	0xe0($key2), $state, $state

XTS

XOR-Encrypt-XOR with Cipher Stealing (XTS) is defined in IEEE 1619, and is a confidentiality only AES mode of operation.

It is the standard encryption used for data at rest.

XTS

XTS sits on top of AES to chain together many 16-byte blocks. In its simplest form, it is literally XOR, AESEncrypt, XOR:

x = zipWith xor twk (take 4 pt)
e = AE.encrypt_ x key
x' = zipWith xor twk e

XTS

XTS sits on top of AES to chain together many 16-byte blocks. In its simplest form, it is literally XOR, AESEncrypt, XOR:

vpxor	$tw, $state, $state

vpxor	($key2), $state, $state
vaesenc	0x10($key2), $state, $state
vaesenc	0x20($key2), $state, $state
vaesenc	0x30($key2), $state, $state
vaesenc	0x40($key2), $state, $state
vaesenc	0x50($key2), $state, $state
vaesenc	0x60($key2), $state, $state
vaesenc	0x70($key2), $state, $state
vaesenc	0x80($key2), $state, $state
vaesenc	0x90($key2), $state, $state
vaesenc	0xa0($key2), $state, $state
vaesenc	0xb0($key2), $state, $state
vaesenc	0xc0($key2), $state, $state
vaesenc	0xd0($key2), $state, $state
vaesenclast	0xe0($key2), $state, $state

vpxor	$tw, $state, $state

XTS

XTS’s initialization vector (IV) is also called a tweak. Between each block’s encryption or decryption, it gets updated.

\[ T' = \begin{cases} (T \ll 1) \oplus \texttt{0x87} & T \gg 127 = 1 \\ T \ll 1 & \text{otherwise} \end{cases} \]

XTS

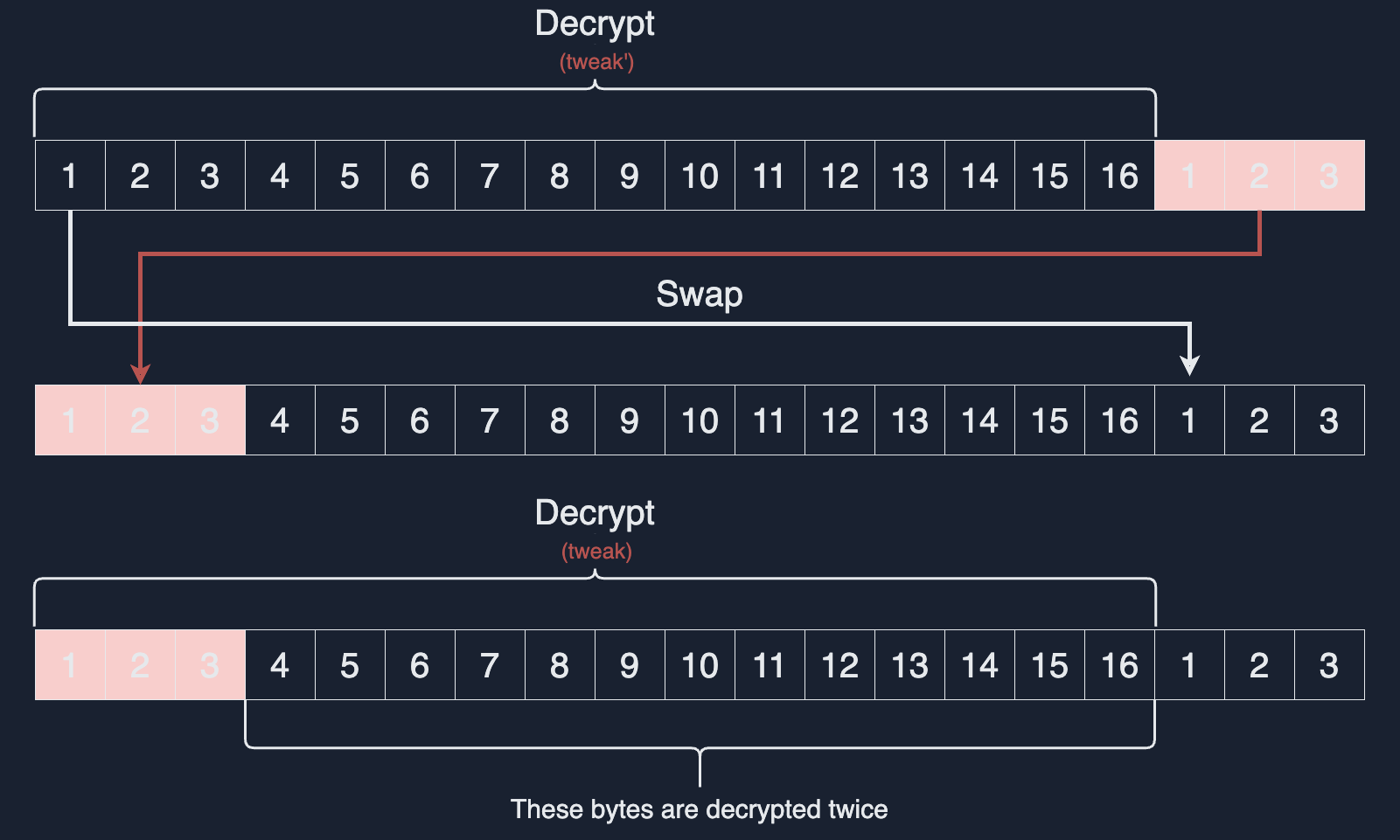
When the input length is not a multiple of 16, cipher stealing is used.

XTS

When the input length is not a multiple of 16, cipher stealing is used.

Recap

AES is a baseline encryption tool, which encrypts (or decrypts) 16-byte blocks at a time.
XTS is a mode of operation, a way of building upon AES’s block cipher for many blocks.
XTS encrypts but does not authenticate and is the standard algorithm used for disk encryption.

Algorithmic Characteristics

AES blocks themselves do not depend on one another in any way, they are isolated pieces of state.
XTS blocks do not depend on the preceding or subsequent blocks of the input.

Vectorization 101

Vectorization is the idea of creating a “vector” of data from a set of scalars, and then using Same Instruction Multiple Data (SIMD) to do a computation on the elements of that vector in parallel.

A scalar is a solitary unit of data, typically a number, say \(7\).
While a vector is collection of scalars:

\[ \mathbf{v} = \begin{bmatrix} 7 \\ 7 \\ 7 \\ 7 \end{bmatrix} \]

Vectorization 101

On x86_64, the %[xyz]mm registers are vector registers.

%xmm registers can hold 128 bits.
%ymm registers can hold 256 bits.
%zmm registers can hold 512 bits.

Vectorization 101

Vectorized instructions are composed of a big pile of mnemonics.

Vectorization 101

vpaddq %ymm0,%ymm1,%ymm1

Where %ymm0 and %ymm1 contain \(\mathbf{v}\) and \(\mathbf{w}\) respectively:

\[ \mathbf{v} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} \\ \]

\[ \mathbf{w} = \begin{bmatrix} 5 \\ 6 \\ 7 \\ 8 \end{bmatrix} \\ \]

Vectorization 101

vpaddq %ymm0,%ymm1,%ymm1

%ymm1 ends up holding:

\[ \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} + \begin{bmatrix} 5 \\ 6 \\ 7 \\ 8 \end{bmatrix} = \begin{bmatrix} 6 \\ 8 \\ 10 \\ 12 \end{bmatrix} \\ \]

Vectorization 101

* Data Independence

* Linearity

Vectorization in XTS

AES blocks in XTS are independent.

vbroadcasti32x4 ($key1), $t0

# ARK
vpternlogq    \$0x96, $t0, $tw1, $st1

# round 1
vbroadcasti32x4 0x10($key1), $t0
vaesenc  $t0, $st1, $st1

# round 2
vbroadcasti32x4 0x20($key1), $t0
vaesenc  $t0, $st1, $st1

# Continued for 14 rounds...

vmovdqu8 	 $st1,($output)

Vectorization in XTS

AES blocks in XTS are independent.

vbroadcasti32x4 ($key1), $t0

# ARK
vpternlogq    \$0x96, $t0, $tw1, $st1
vpternlogq    \$0x96, $t0, $tw2, $st2

# round 1
vbroadcasti32x4 0x10($key1), $t0
vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2

# round 2
vbroadcasti32x4 0x20($key1), $t0
vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2

# Continued for 14 rounds...

vmovdqu8 	 $st1,($output)
vmovdqu8 	 $st2,0x40($output)

Vectorization in XTS

AES blocks in XTS are independent.

vbroadcasti32x4 ($key1), $t0

# ARK
vpternlogq    \$0x96, $t0, $tw1, $st1
vpternlogq    \$0x96, $t0, $tw2, $st2
vpternlogq    \$0x96, $t0, $tw3, $st3
vpternlogq    \$0x96, $t0, $tw4, $st4

# round 1
vbroadcasti32x4 0x10($key1), $t0
vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2
vaesenc  $t0, $st3, $st3
vaesenc  $t0, $st4, $st4

# round 2
vbroadcasti32x4 0x20($key1), $t0
vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2
vaesenc  $t0, $st3, $st3
vaesenc  $t0, $st4, $st4

# Continued for 14 rounds...

vmovdqu8 	 $st1,($output)
vmovdqu8 	 $st2,0x40($output)
vmovdqu8 	 $st3,0x80($output)
vmovdqu8 	 $st4,0xc0($output)

Vectorization in XTS

Tweak generation in XTS does have “some” linearity.

If:

\[ T' = \begin{cases} (T \ll 1) \oplus \texttt{0x87} & T \gg 127 = 1 \\ T \ll 1 & \text{otherwise} \end{cases} \]

Then:

\[ T'' = \begin{cases} (T \ll 2) \oplus \texttt{0x87} & T \gg 126 = 1 \\ T \ll 2 & \text{otherwise} \end{cases} \]

Vectorization in XTS

Tweak generation in XTS does have “some” linearity.

# Tweaks 0-3
vpsllvq const_dq3210(%rip),%zmm0,%zmm4
vpsrlvq const_dq5678(%rip),%zmm1,%zmm2
vpclmulqdq 	 \$0x0,$ZPOLY,%zmm2,%zmm3
vpxorq 	 %zmm2,%zmm4,%zmm4{%k2}
vpxord 	 %zmm4,%zmm3,%zmm9

Bonus Optimizations

Instruction-Level Parallelization

vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2
vaesenc  $t0, $st3, $st3
vaesenc  $t0, $st4, $st4

Bonus Optimizations

Why four?

\[ \text{Parallelism} = \text{Cycle Latency} \times \text{IPC} \]

\[ 8 = 4 \times 2 \]

Bonus Optimizations

Why four?

Bonus Optimizations

Instruction-Level Parallelization

# round 3
vbroadcasti32x4 0x30($key1), $t0
vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2
vaesenc  $t0, $st3, $st3
vaesenc  $t0, $st4, $st4

# Generate next 4 tweaks
vpsrldq		\$0xf, $t0, %zmm13
vpclmulqdq	\$0x0,$ZPOLY, %zmm13, %zmm14
vpslldq		\$0x1, $t0, %zmm16
vpxord		%zmm14, %zmm16, %zmm16

# round 4
vbroadcasti32x4 0x40($key1), $t0
vaesenc  $t0, $st1, $st1
vaesenc  $t0, $st2, $st2
vaesenc  $t0, $st3, $st3
vaesenc  $t0, $st4, $st4

Bonus Optimizations

Instruction-Level Parallelization

# Tweaks 0-3
vpsllvq const_dq3210(%rip),%zmm0,%zmm4
vpsrlvq const_dq5678(%rip),%zmm1,%zmm2
vpclmulqdq 	 \$0x0,$ZPOLY,%zmm2,%zmm3
vpxorq 	 %zmm2,%zmm4,%zmm4{%k2}
vpxord 	 %zmm4,%zmm3,%zmm9

# Tweaks 4-7
vpsllvq const_dq7654(%rip),%zmm0,%zmm5
vpsrlvq const_dq1234(%rip),%zmm1,%zmm6
vpclmulqdq 	 \$0x0,$ZPOLY,%zmm6,%zmm7
vpxorq 	 %zmm6,%zmm5,%zmm5{%k2}
vpxord 	 %zmm5,%zmm7,%zmm10

References

crypto-ref: reference implementations of AES and XTS. This is where the Haskell code samples in this presentation come from.
AWS-LC: the optimized AES-XTS implementation referenced in this presentation.
FIPS 197: the standard defining AES.
IEEE 1619: the standard defining XTS mode.
Notes on vectorized XTS: this includes the expanded vectorized tweak generation discussed in this presentation, with comments added line-by-line explaining each step.